How to use Linear Regression Calculator?

Linear regression calculator documentation

Definition of linear regression

It is a type of statistical method used to find a linear relationship between two variables - independent and dependent one. This method is also called "simple linear regression". There is also multiple linear regression - when the linear relationship is to be found between more than one independent variables and one dependent variable.

The best-fitting line is obtained by minimizing the sum of the squared errors, that is differences between the predicted and the actual values.

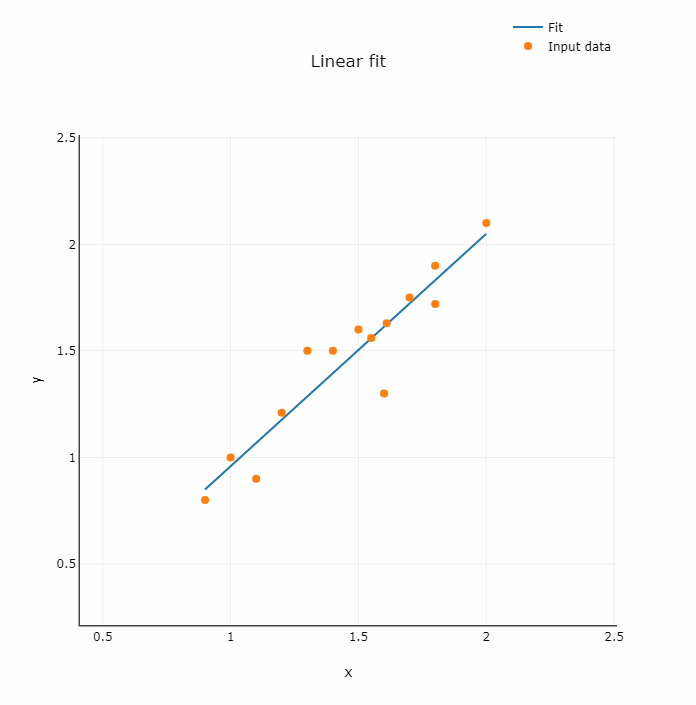
Chart of regression line fitted to data

Linear regression equation

The equation of regression line is:

$y = a + b \cdot x$

where:

a - intercept

b - slope

x - independent variable

y - dependent variable

You can use our tool as linear regression calculator by choosing "Linear fit" from the dropdown menu ("Choose fit method"). The calculator will automatically determine the regression equation with coefficients.

How to calculate linear regression?

The regression coefficient b is given by:

$b=\frac{SS_{xy}}{SS_{xx}}=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^{n}(x_i-\bar{x})^2}$

and a is calculated in terms of b as

$a=\bar{y}-b\bar{x}$

Where linear regression analysis is used?

Linear regression analysis is a fundamental technique in statistics and it has a wide range of applications across various fields. It is used for example in economy, social sciences, data science, sport analytics and engineering. Linear regression can also help analyze various phenomena, for example in environmental science or in manufacturing industry.

Least squares method

It is a method is a mathematical procedure for finding the best-fitting curve to a given set of points. It is based on minimizing the sum of the squares of the the residuals of the points from the curve (SSE - Sum of Squared Error). It is defined as:

$SSE = \sum_{i=1}^{n}[y_i - \bar{y}_i]^2$

where:

$y_i$ - value of y at point i

$\bar{y}_i$ - predicted value of y at point i

The function SSE is minimized to find the best fit line.

The condition for SSE to be a minimum is:

$\frac{\partial SSE}{\partial a_i}=0$

for i = 1,...,n

Measures of goodness

R squared

Coefficient of determination also denoted $R^2$ is a statistical measure which shows how well the regression model fits the data. It represents the proportion of variance in the dependent variable that can be explained by the independent variable. The formula for calculating $R^2$ is:

$R^2=1-\frac{\text{Unexplained Variation}}{\text{Total Variation}}$

Typically, $R^2$ is in the range of 0 and 1. A higher $R^2$ value (closer to one) imply that more variation is explained by the model. An $R^2$ of 1 indicates that the model predictions perfectly fit the observed data. It is worth to note that the coefficient of determination is the square of the correlation coefficient.

Sum of Squared Errors (SSE)

The sum of squared errors is defined as:

$SSE = \sum_{i=1}^{n}[y_i - \bar{y}_i]^2$

The value of SSE is minimized in order to find coefficients of a best-fitting curve.

How to use the calculator?

Data input

User inputs the data into the table. There are two columns X and Y with exemplary data loaded. Insert the value into the table by selecting a cell, typing a number and pressing enter.

Perform analysis

The analysis is run automatically, after introducing X and Y values.

Draw chart

A chart is also created automatically, when you put your data to the table. The chart is interactive. There are two data sets shown automatically. You can hide any of them by clicking on the proper name on the legend in the top right corner of the diagram. You can also see the values of any point by moving the cursor to that point. Save the chart as png file by choosing the option "Download plot as a png".

Line of best fit

The regression line is in the "Result" section. The coefficients found are automatically introduced to the equation. For example, if the calculator finds: a = 2.1 and b = 3.5, then the result looks like this:

$y = 2.1+3.5x$

Export the results of the linear regression calculator

You can choose one of two methods. First one, "PRINT" will open window allowing for printing whole analysis or saving it as a PDF File. The second one, "Export TXT Report" is to save the results as txt. It is a convenient way, as the file created contains the copyable equation in latex format and fitted values.