Continuous Stirred Tank Reactor (CSTR)

Introduction

CSTR (Continuous Stirred-Tank Reactor) is a type of chemical reactor used in the industry for various chemical and biochemical processes. In a CSTR, reactants are continuously fed into a tank, and the reacting mixture is continuously withdrawn from the reactor. The content of the tank is well mixed to ensure a uniform composition.

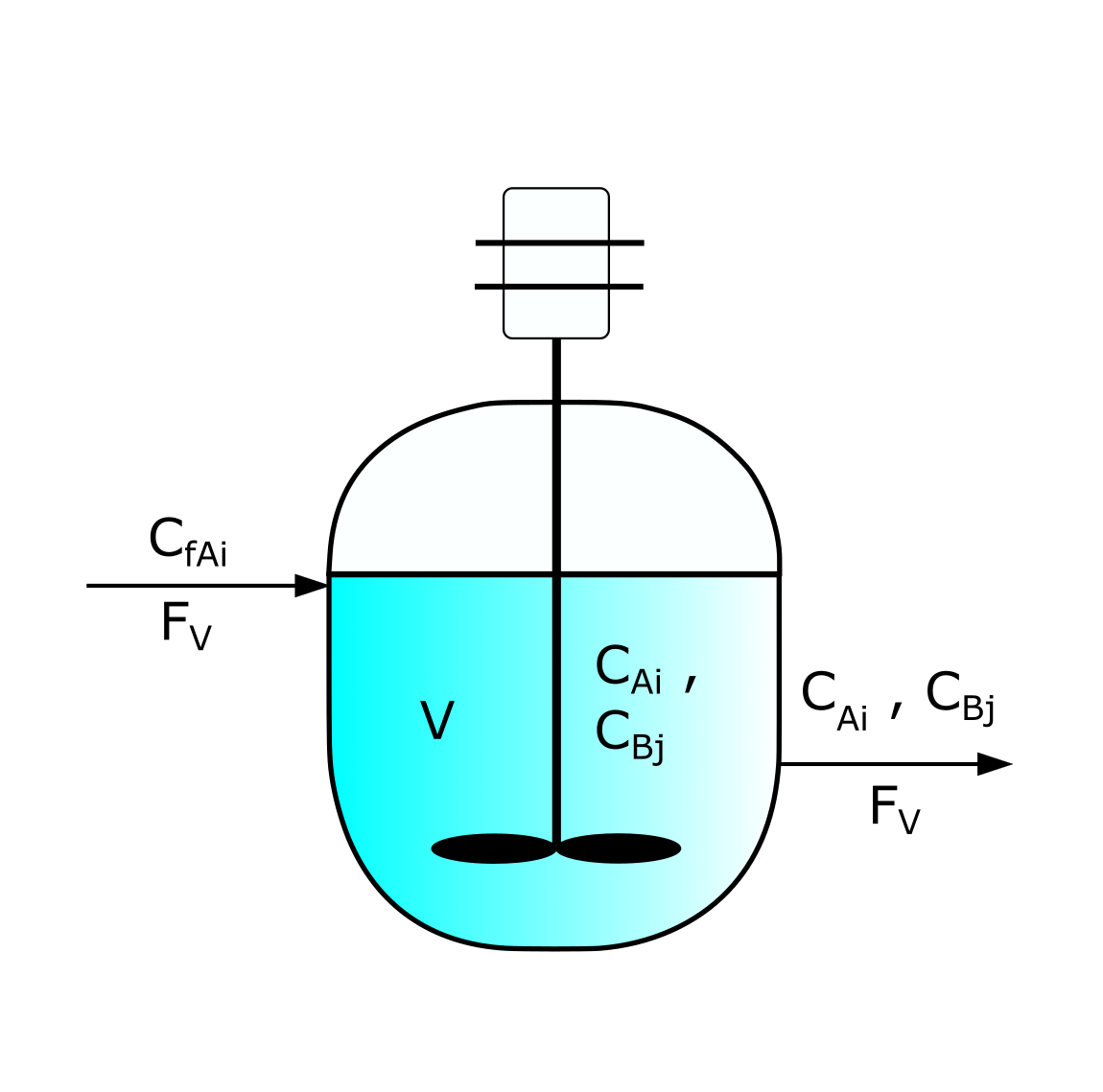
Fig. 1. Scheme of a CSTR

Mathematical model of CSTR

Model of isothermal CSTR is based on mass balance of reagents. Number of equations depends on the complexity of the chemical reaction or system of reactions. When we deal with simple irreversible reaction A→B then there will be one equation describing mass balance of substrate A, as below.

$$V\frac{dC_A}{dt}=F_VC_{Af}-F_VC_{A}-V\cdot r(C_A) \tag{1}$$

where:

$C_A$ - concentration of substrate A inside the reactor, $mol\text{ }A/s$

$C_{Af}$ - concentration of substrate A in the inflow stream, $mol\text{ }A/s$

$F_V$ - volumetric flow rate, $m^3/s$

$r$ - reaction rate, $mol\text{ }A/(m^3s)$

$t$ - time, s

$V$ - volume, $m^3$

The interpretation of the equation (1) is following: Each term in the equation is expressed in units of [mol A/s]. Terms on the right sum together to the term on the left-hand-side, which is the accumulation rate of substrate A in the volume V of the reactor. The first term on the right-hand-side of the equation is the substrate A inflow rate. The second term is the outflow rate of A. We can see that the concentration in this stream is the same as inside the reactor. It's because the ideal CSTR is assumed to be perfectly mixed, so the concentration of A is the same inside the entire reactor. The last term is the substrate uptake due to chemical reaction. The expression $r$ depends on the type of the reaction. For example, if we deal with A→B reaction, then we have:

$$r(C_A) = k\cdot C_A \tag{2}$$

After introducing Eq. (2) to Eq. (1) and simplifying, we get:

$$\frac{dC_A}{dt}=\frac{F_V}{V}C_{Af}-\frac{F_V}{V}C_{A}-kC_A \tag{3a}$$

or

$$\frac{dC_A}{dt}=\frac{1}{\tau}(C_{Af}-C_{A})-kC_A \tag{3b}$$

Coefficient $\tau$ in the above equation is called a mean residence time, and is calculated as a ratio of volume to volumetric flow rate $\tau = \frac{V}{F_V}$.

To solve the the differential equation we need to know initial condition. In this case, it is the initial concentration $C_A(0)$:

$$C_A(0)=C_{A0} \tag{4}$$

The above problem is called an initial value problem or Cauchy problem. You can read how to solve it in Python language on our blog (solving differential equations in Python).

The Eq. (3) is a dynamic model of CSTR, so it describes its operation before reaching the steady state. However, more common situation concerns steady-state operation. From modeling point of view, reaching a steady state means $\frac{dC_A}{dt}=0$. So, the differential equation will reduce to algebraic equation:

$$0=\frac{1}{\tau}(C_{Af}-C_{A})-kC_A \tag{5}$$

Design of CSTR

Let's consider the following example, in which we want to achieve given concentration of substrate A in the outlet stream. As CSTR is operated in steady state, we will use Eq. (5). Simple transformation results in expression for calculating $\tau$:

$$\tau =\frac{(C_{Af}-C_{A})}{kC_A } \tag{6}$$

The calculated mean residence time ensures reaching assumed $C_A$. In turn, the value $\tau$ can be obtained by changing volume or volumetric flow rate, depending on process requirements. For example, if we know the volumetric flow rate, we can calculate reactor volume according to the relationship:

$$V = \tau F_V \tag{7}$$

Analogously, we can use Eq. (5) to calculate concentration A for a given volume and volumetric flow rate:

$$C_{A}=\frac{C_{Af}}{(1+\tau k)} \tag{8}$$

How to use the CSTR Online Simulation Tool

The usage of CSTR simulator is very simple. Just type the parameters into the table, ane the results will be calculated automatically. The full tutoral how to use the CSTR simulator: https://youtu.be/UiB6bwUXHp8

A convenient way to introduce the parameters is to read a file. The parameters should be specified as below:

{
	"kinetic_constant": 0.114,
	"time": 100,
	"volume": 24,
	"volumetric-flow-rate": 0.61,
	"N_A": 1,
	"N_B": 1,
	"initial-concentrations": [2.5],
	"inlet-concentrations": [1.5],
	"table-ni-a": [3],
	"table-ni-b": [2],
	"table-orders-a": [0.5]
}

Short tutorial how to import parameters from a file is presented in the video: https://youtu.be/KuX_OWMH9DE

The interface of the application looks like this:

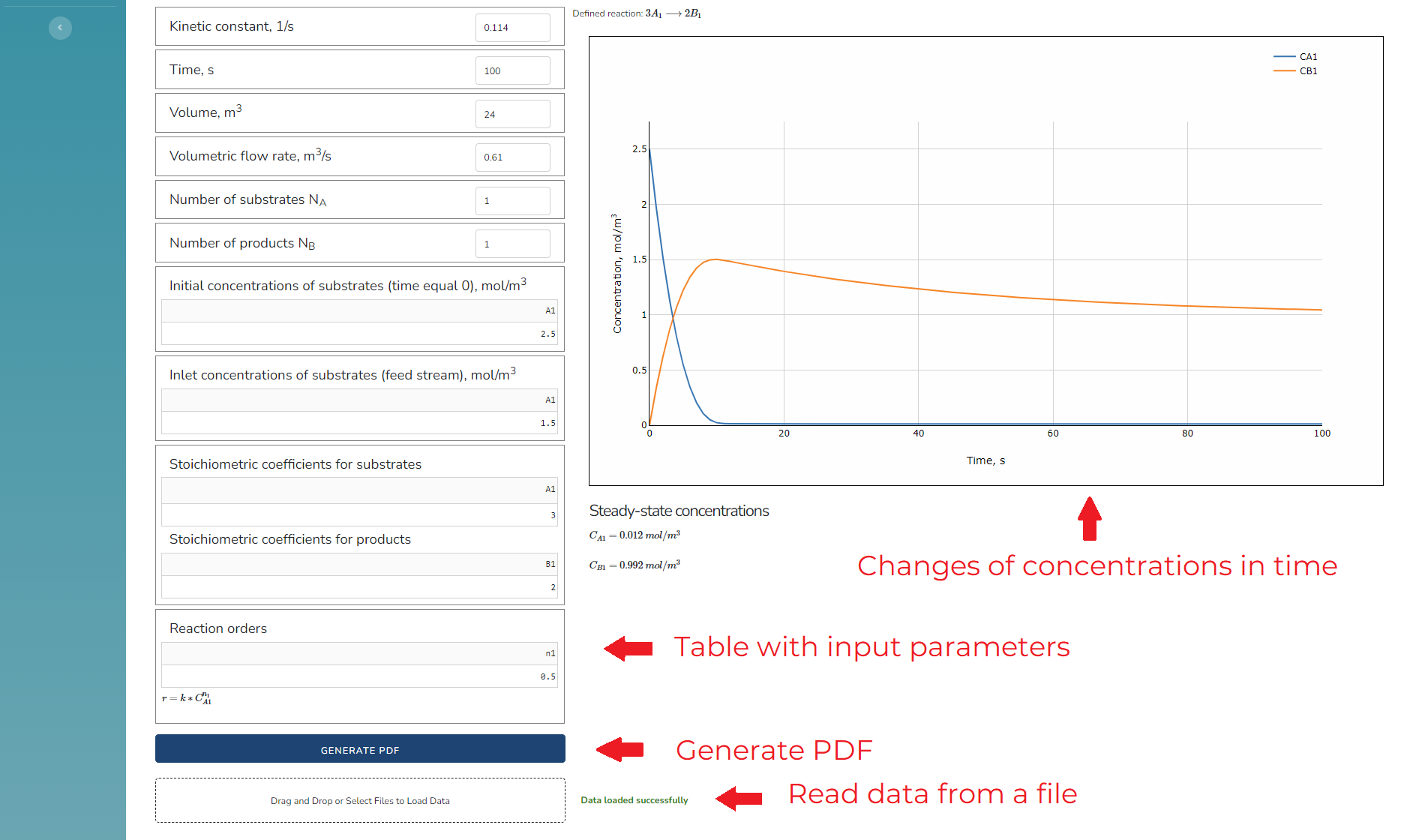
Fig. 2. CSTR Online Simulation Tool interface