Documentation of non-isothermal batch reactor simulation

Introduction

A batch reactor is a widely used type of reactor in chemical engineering, where all reactants are loaded into the reactor at the beginning of the process, and the reaction proceeds in a closed system without any inflow or outflow of materials during operation. Unlike continuous reactors, where the system operates under steady-state conditions, batch reactors are inherently transient, meaning that concentrations, temperature, and reaction rates vary over time.

In many real-world applications, chemical reactions are either exothermic (release heat) or endothermic (absorb heat), leading to significant temperature changes within the reactor. This introduces the concept of non-isothermal operation, where the reactor temperature is not constant but evolves as a result of the heat generated or consumed by the reaction.

Non-isothermal batch reactors are particularly challenging to model and control because the reaction rate is strongly influenced by temperature, which in turn is affected by the rate of heat transfer and accumulation. Understanding the interaction between heat generation, heat removal, and the kinetics of the chemical reaction is essential for designing safe and efficient operation. Inadequate temperature control in such systems can lead to runaway reactions or low conversion.

The study of non-isothermal batch reactors typically involves the coupling of mass and energy balances. By solving these coupled equations, engineers can predict the behavior of the system, optimize reaction conditions, and ensure process safety.

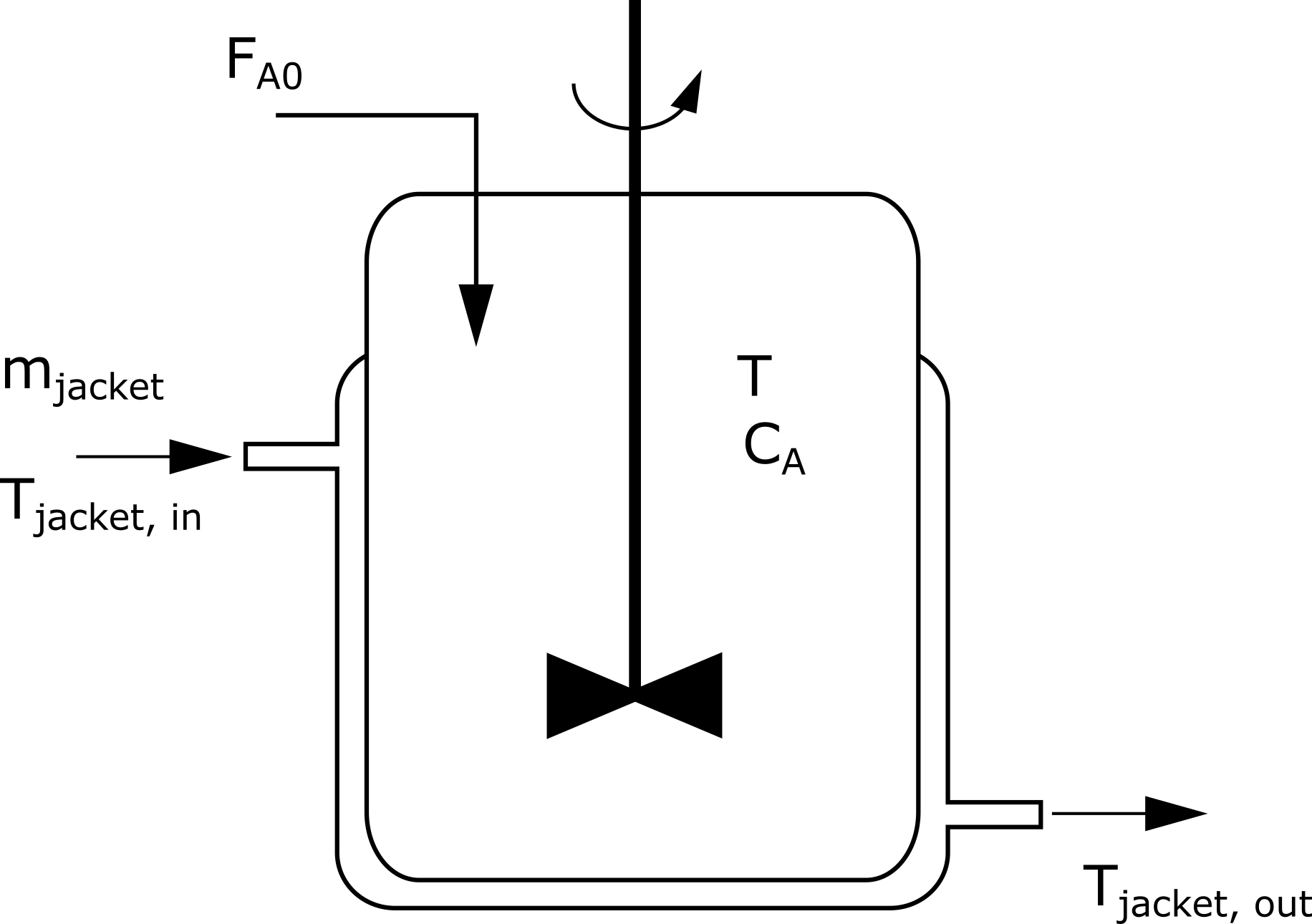
Fig. 1. Scheme of a non-isothermal batch reactor

A mathematical model of a non-isothermal batch reactor

The mathematical model of a non-isothermal batch reactor consists of mass balance and heat balance equations.

Mass balance equation

Let's first consider a first-order irreversible reaction:

$$A \to Products \tag{1}$$

with kinetic expression:

$$r_A(C_A) = k(T) \cdot C_{A} \tag{2}$$

where:

$r_A$ is the uptake rate of reactant A, $mol/(m^3s)$,

$C_A$ is the reactant A concentration, $mol/m^3$,

$k$ is the kinetic constant, 1/s for first-order reaction.

The rate constant depends on the temperature according to the Arrhenius equation:

$$k = k_0 e^{\frac{-E_a}{RT}} \tag{3}$$

where:

$E_a$ - activation energy, $kJ/mol$

$k$ - rate constant of the reaction, units vary depending on the order of the reaction (e.g., $s^{−1}$ for first-order reactions, $m^3 \cdot mol^{−1} \cdot s^{−1}$ for second-order reactions),

$k_0$ - pre-exponential factor with the same units as $k$, $R$ - universal gas constant, 8.314 $J \cdot mol^{-1} \cdot K^{-1}$

$T$ - temperature, K

For a single irreversible chemical reaction, the model will consist of one mass balance equation. To formulate this equation, we need to consider balance volume equal to reaction volume V, which is a typical procedure in modeling tanks equipped with an impeller. This means we assume perfect mixing in the tank. The left-hand-side of the mass balance equation (3) is the accumulation rate in volume V, while the right-hand side is the uptake rate of the reactant A. As there is no inflow or outflow to the reactor, there will be no additional terms in this equation.

$$V\frac{dC_A}{dt}=-V \cdot r_A(C_A, T) \tag{4}$$

where:

$t$ is time, s,

$V$ is the reactor volume, m³.

Heat balance equation

The heat balance equation is the following:

$$V \rho c_p \frac{dT}{dt} = V \cdot r_A(C_A, T) (- \varDelta H_A ) - A_q k_q (T - T_q) \tag{5}$$

where:

$\rho$ - density of the liquid or gas in the reactor, $kg/m^3$

$c_p$ - specific heat capacity of the liquid or gas, $kJ/(kgK)$

$\varDelta H_A$ - enthalpy of reaction for species $A$, $kJ/mol A$

$A_q$ - heat transfer area (e.g., surface area of the reactor), $m^2$

$k_q$ - heat transfer coefficient between the reactor and coolant, $W/(m^2K)$

$T_q$ - temperature of the coolant, $K$

Simplification of the non-isothermal batch reactor model

After reducing volume V in Eq. (4), we get:

$$\frac{dC_A}{dt}=-r_A(C_A,T) \tag{6}$$

After dividing Eq. (5) by $V \rho c_p$:

$$\frac{dT}{dt} = \frac{(- \varDelta H_A)}{\rho c_p} \cdot r_A(C_A, T) - \frac{A_q k_q}{V \rho c_p} (T - T_q) \tag{7}$$

To solve the above system of equations (6)-(7), initial conditions are required. In this case, they are the initial concentration of the reactant A and the initial temperature inside the reactor:

$$C_{A} (0) = C_{A0} \tag{8a}$$

$$T (0) = T_{0} \tag{8b}$$

Different reaction orders

Equations (6)-(7) with conditions (8) will also be suitable for zero-order kinetics or higher-orders kinetics if there is only one reactant. For example, if we deal with zero-order chemical reaction, the kinetic expression will be the following:

$$r_{A} = k(T) \tag{9}$$

For second-order chemical reactions, the kinetic expression will be:

$$r_{A} = k(T) \cdot C_{A}^{2}\tag{10}$$

and so on.

When there is more than one reactant, the mathematical model gets more complex. Namely, we need to extend it by further mass balance equations. Let's consider the following chemical reaction:

$$A + B \to Products \tag{11}$$

For this chemical reaction, the kinetic expressions are:

$$r_A(C_A, C_B) = k(T) \cdot C_{A} \cdot C_{B}\tag{12a}$$

$$r_B(C_A, C_B) = k(T) \cdot C_{A} \cdot C_{B}\tag{12b}$$

The above equations can be completed by introducing orders of the reactions, if necessary.

For such a reaction, the mathematical model will consist of two mass balance equations and heat balance, formulated on the same basis as previously:

$$\frac{dC_A}{dt}=-r_A(C_A, C_B, T) \tag{13a}$$

$$\frac{dC_B}{dt}=-r_B(C_A, C_B, T) \tag{13b}$$

$$\frac{dT}{dt} = \frac{(- \varDelta H_A)}{\rho c_p} \cdot r_A(C_A, C_B, T) - \frac{A_q k_q}{V \rho c_p} (T - T_q) \tag{7}$$

Three initial conditions are required to solve the model. In this case, they are the initial concentrations of A and B and the initial temperature inside the reactor:

$$C_{A} (0) = C_{A0} \tag{14a}$$

$$C_{B} (0) = C_{B0} \tag{14b}$$

$$T (0) = T_{0} \tag{14c}$$

The above reasoning can be extended to more complex reactions. In general, we can deal with stoichiometric coefficients and reaction orders different than one. For example:

$$aA + bB \to Products \tag{12}$$

with kinetic expressions:

$$r_A(C_A, C_B, T) = a \cdot k(T) \cdot C_{A}^{n_1} \cdot C_{B}^{n_2}\tag{13a}$$

$$r_B(C_A, C_B, T) = b \cdot k(T) \cdot C_{A}^{n_1} \cdot C_{B}^{n_2}\tag{13b}$$

Despite the fact that the mass balance of a product is not necessary to solve the mathematical model, it might be interesting to find its concentration. To do this, we need to append an additional equation:

$$\frac{dC_P}{dt}=r_P(C_A, C_B, T) \tag{14}$$

where:

$$r_P(C_A, C_B) = p \cdot k(T) \cdot C_{A}^{n_1} \cdot C_{B}^{n_2}\tag{15}$$

and

$$C_{P} (0) = C_{P0} \tag{16}$$

and p denotes the stoichiometric coefficient for the product P.

Non-isotherma batch reactor design

The goal of batch reactor design can be specified in two ways. The first one is when we want to run the process for a given time. In such a case, we need to solve the model for this value of time. Assuming we deal with the $A \to B$ reaction, the result we obtain consists of two functions:

$$C_A(t) \tag{17a}$$

$$C_B(t) \tag{17b}$$

The values at the final time represent the consentrations when the process is finished.

In another scenario, we want to obtain a chosen concentration of a reactant or product after the process. In this case, we solve the mathematical model and read the time from the diagram. This process can be automated, but this will not be discussed in this documentation.

Non-isothermal batch reactor simulation

The simulation in the Sofinery application is very easy. The process parameters are introduced into the table. They include:

• time of the process,
• number of substrates,
• number of products,
• pre-exponential factor,
• activation energy,
• initial temperature,
• initial concentrations of substrates,
• stoichiometric coefficients for substrates,
• stoichiometric coefficients for products,
• reaction orders,
• physicochemical properties of reaction mixture: density, specific heat,
• reaction enthalpy,
• cooling medium temperature,
• heat transfer area,
• heat transfer coefficient.

After introducing the parameters, the simulation is performed automatically. According to the input, the reaction is updated. The result of the simulation is visualized on the diagram in the form of kinetic curves, that is, the relationships of concentrations vs. time.

References

[1] Levenspiel, Octave. Chemical reaction engineering. John Wiley & Sons, 1998. Link

[2] Nauman, E. Bruce. Chemical reactor design, optimization, and scaleup. John Wiley & Sons, 2008. Link